Group Actions and Orbit Spaces
This article continues the concepts introduced in the one on quotient spaces. Here I will use group actions and their properties to create quotients of a square.
Definitions
When an underlying set of a topological space is endowed with an operator such that it satisfies the group axioms, we end up with a structure that is called a topological group. The remarkable thing about these groups is that we can now apply all group-theoretic properties to our topological contexts.
A group action of a group \(G\) on a space \(X\) is a function \(\phi: G \times X \to X\) which satisfies the following properties:
- Identity: For all \(x \in X\), \(\phi(e, x) = x\) where \(e \in G\) is the identity element for the group
- Compatibility: For any \(g, h \in G\), \(\phi(gh, x) = \phi \left( g, \phi(h, x) \right)\)
In other words, for a fixed \(g \in G\), we get a bijective map on \(X\). These actions can be used to partition the space \(X\). We define an orbit of an element \(x \in X\) to be the set \[ O_x = \lbrace g \circ x \vert g \in G \rbrace \] Here I have used \(g \circ x\) as a shorthand for \(\phi(g, x)\). A better way to understand orbits would be to state that \(y \in O_x\) implies that there exists some \(g \in G\) which results in a bijection that takes \(x\) to \(y\). It can easily be verified that these orbits indeed create a partition of \(X\). The underlying equivalence relation that we’re using is that \(x \sim y\) if \(y \in O_x\).
In the last article, we studied the example of rolling a real line into a circle. This can be thought of as a group action of \( (\mathbb{Z}, +) \) on \(\mathbb{R}\) defined by \(z \circ x = z + x\), where \(z \in \mathbb{Z}\) and \(x \in \mathbb{R}\).
Quotients of a square
We have already seen a way to create a torus by rolling a sheet of paper. Different partitions create different spaces, but it turns out that there are exactly four unique ones. This means that any partition on this sheet will create a space that is homeomorphic to one of these four: sphere, torus, Klein bottle or a projective plane. The square, in this case, is a fundamental polygon of these four spaces.
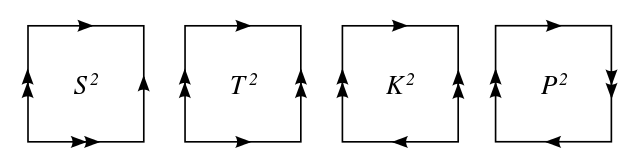
The four unique ways to partition a square. Source.
These four partitions can be created using group actions by identifying pairs of points as one. This is mathematically equivalent to defining a group action of the group \(\mathbb{Z}_2\), the set of integers modulo \(2\), on the square. Assume that the square is given by \([-1, 1] \times [-1, 1]\) and define the action
\[ \begin{aligned} 0 \circ (x, y) &= (x, y) \cr 1 \circ (x, y) &= \begin{cases} (x, -y) & x \neq 1 \cr (-x, y) & x = 1 \end{cases} \end{aligned} \]
Now from each orbit, let’s pick the point with \(x = 1\) or \(y > 0\) if \(x \neq 1\). This leaves us with \((-1, 1] \times (0, 1]\), the top half of the square with some edges excluded. Because of these excluded edges, we can now define a homeomorphism that warps this sheet into a tube and then warps that tube into a torus.
For another example, we can look at an action of \(\mathbb{Z}_2\) on a torus itself. Consider a torus in \(\mathbb{R}^3\) that is centred at the origin and is along the XY-plane. Define the action by
$$ \begin{aligned} 0 \circ (x, y) &= (x, y) \cr 1 \circ (x, y) &= g(x, y, z) = (-x, -y, z) \end{aligned} $$
Now if we pick points from the orbits of this action, we will get half a torus whose ends can be joined to create a new torus. This second example is convenient because by changing the function \(g\), we can create new shapes. For a sphere, use \(g(x, y, z) = (x, -y, -z)\) and for a Klein Bottle, use \(g(x, y, z) = (-x, -y, -z)\).
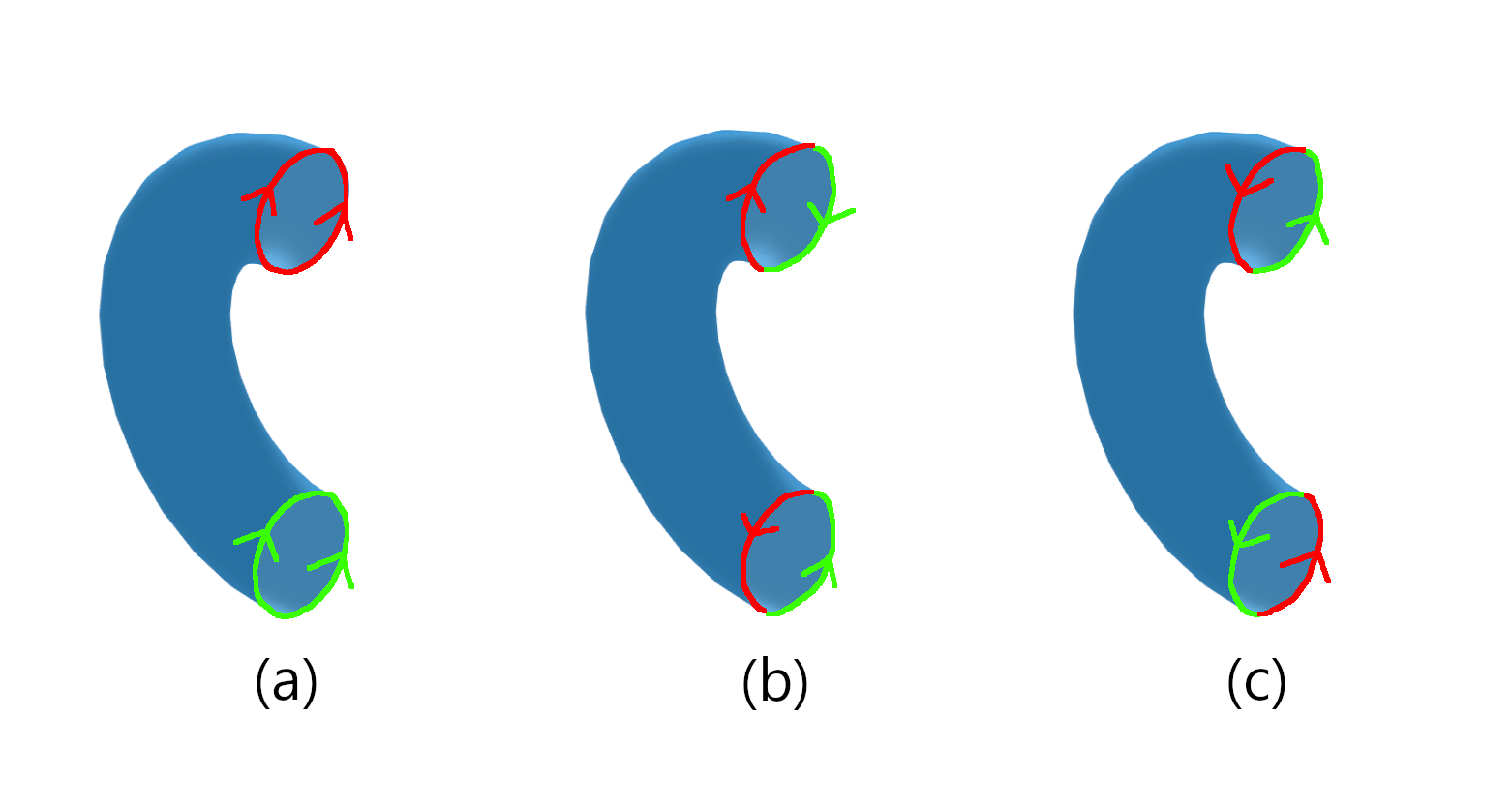
Identification of points using actions of \(\mathbb{Z}_2\) on a torus. (a) Sphere (b) Torus and (c) Klein bottle.
Creating these three shapes from our square was a two-step process. First, roll the square into a tube and then, join the ends of this tube in a particular way. This second step is what \(g\) represents. To get a projective plane though, we don’t need the tube. If you consider the square to be a disk (they’re homeomorphic), then the way that we identify points on the square is as if we were identifying antipodal points on a disk. This is precisely what our group action will do. Define an action of \(\mathbb{Z}_2\) on the closed unit disk as follows, to create a partition equivalent to the square construction above.
\[ \begin{aligned} 0 \circ (x, y) &= (x, y) \cr 1 \circ (x, y) &= (-x, -y) \end{aligned} \]